–> Clicca qui per la bibliografia
Lo studio del diagramma di Nyquist della F(s) risulta di particolare importanza perché non si limita a fornire un’indicazione “on/off” ( stabile/instabile ) sulla stabilità del sistema retroazionato , ma permette al progettista un’analisi più complessa sul comportamento del sistema stesso al variare del guadagno statico in catena aperta. Le fasi di questa analisi sono due:
| 1) | Classificazione della stabilità , in 4 categorie ; facendo riferimento , per semplicità , alla situazione di un sistema a retroazione unitaria ( per cui il punto critico è -1+j0 ) e di sistema in catena aperta stabile ( per cui si applica il criterio di Nyquist ridotto , la condizione di instabilità si riconduce al circondamento del punto critico da parte del diagramma polare ) , alle 4 categorie corrispondono altrettanti comportamenti del diagramma di Nyquist al variare del guadagno : |
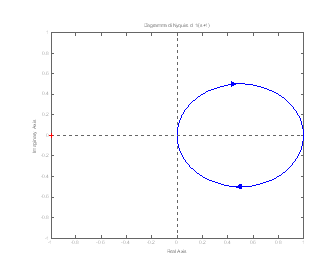
| 1a) stabilità incondizionata se, come visto nell’esempio del paragrafo precedente , il sistema è stabile per qualsiasi valore del guadagno statico. Sistemi di questo tipo sono caratterizzati da un diagramma di Nyquist che non interseca mai il semiasse reale negativo. Questa situazione è riportata in figura 1. | |
 | |
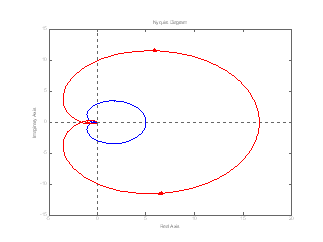
| 1b) stabilità regolare , se il sistema risulta stabile per un intervallo di guadagni Kst che va da 0 ad un valore limite Kmax . Rientrano in questa categoria i sistemi il cui diagramma di Nyquist interseca in un solo punto il semiasse reale negativo : nelle figure 3 e 4 sono mostrati i diagrammi di un sistema a tre poli reali negativi del tipo | |
 | |
| rispettivamente per Kst=30 ( in blu , in corrispondenza del quale il diagramma non circonda il punto critico e quindi il sistema retroazionato è stabile ) e per Kst=100 ( in rosso , in corrispondenza del quale il diagramma circonda il punto critico e quindi il sistema retroazionato è instabile ). | |
  {loadposition adsense_negli_articoli} | |
| 1c) stabilità condizionata , se il sistema risulta instabile tanto per Kst<Kmin che per Kst>Kmax : esiste quindi un intervallo di valori che il progettista può assegnare al guadagno statico in modo da ottenere un sistema retroazionato stabile. Al di fuori di tale intervallo il sistema a ciclo chiuso risulta instabile. Questi sistemi sono caratterizzati da un diagramma di Nyquist che interseca in più punti il semiasse reale negativo , in modo che il punto critico venga circondato tanto per piccoli valori di Kst , che per grandi valori di Kst. Quando le intersezioni con il semiasse negativo sono molte, può anche accadere che esistano più intervalli di stabilità per il guadagno statico : perché però l’applicazione del criterio mantenga significato fisico è necessario che ciascuno di questi intervalli sia limitato superiormente. Altrimenti si parla di : | |
| 1d) stabilità paradossale , quando , per Kst>kn , il diagramma non circonda più il punto critico e quindi il sistema retroazionato è stabile anche per valori indefinitamente grandi del guadagno statico . Si parla di stabilità paradossale perché questa situazione è sintomo di un errore nello studio del sistema stesso : un motivo frequente è ad esempio un’eccessiva semplificazione nell’identificazione del modello della F(s) , che induce a trascurare poli non irrilevanti nella dinamica del sistema stesso.{loadposition adsense_negli_articoli} | |
| 2) | Quantificazione della stabilità , mediante la definizione dei margini di stabilità . Non è infatti sufficiente , ai fini della sintesi di un sistema di controllo, affermare che il sistema progettato è stabile : bisogna specificare quanto il sistema realizzato è lontano dalla condizione di instabilità . Se infatti il sistema progettato è , già “sulla carta”, prossimo al limite di instabilità , ci si può ritrovare, “sul campo “, con un sistema di fatto instabile a causa di diversi fattori : – approssimazioni adottate in fase di progetto ; – variazioni parametriche rispetto al modello considerato ; – insorgenza di disturbi non preventivati. Si è detto in precedenza che , per sistemi stabili in catena diretta , la condizione di instabilità è rappresentata dal circondamento , da parte del diagramma di Nyquist , del punto critico ( -1+j0 , nel caso di retroazione unitaria ) : a partire da questa osservazione si sono definiti due parametri che permettano la quantificazione di cui sopra. |
{loadposition adsense_negli_articoli}2a) margine di guadagno : riferendoci per semplicità ad un sistema del tipo 1a) , al crescere di Kst l’intersezione del diagramma con il semiasse reale negativo si avvicina al punto -1+j0 , fino a circondarlo in corrispondenza di un valore Kst=kmax. Dicendo  la frequenza per cui avviene tale intersezione ( cioè  ) , la distanza fra tale punto ( indicato in figura 4 con la lettera P ) e -1+j0 ( indicato in figura 4 con la lettera C ) è una buona misura di quanto il sistema sia distante dall’instabilità. Tale quantità , che è rappresentata in figura 4 dal segmento PC e si può valutare matematicamente come  , è una prima possibile definizione del margine di guadagno. | |
 | |
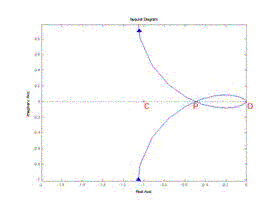Non si tratta tuttavia della definizione più utilizzata , pertanto si è indicato questo paramentro con mg’ . La soluzione più diffusa consiste infatti nel definire il margine di guadagno come il rapporto fra il segmento OP ed il segmento OC :  Trattando sistemi a retroazione unitaria si ha OC=1 , perciò il margine di guadagno si riduce a : Il motivo del maggiore utilizzo di mg a scapito di mg’ risiede nel fatto che , essendo un rapporto, mg si può esprimere anche in dB ed è direttamente rilevabile dai diagrammi di Bode della funzione di trasferimento:  ;Per i sistemi a retroazione unitaria il logaritmo di OC è nullo e quindi il margine di guadagno si riduce a : Si noti che OP è il modulo della funzione di trasferimento in corrispondenza dell’intersezione con il semiasse reale negativo , quindi per sistemi stabili ha valori inferiori all’unità : il logaritmo è quindi negativo e il margine di fase è positivo. Per sistemi a retroazione unitaria instabili, invece, tale segmento ha ampiezza maggiore di 1 e il corrispondente logaritmo è positivo : il margine di fase è negativo. | |
| {loadposition adsense_negli_articoli}2b) margine di fase : la figura 5 mostra che il margine di guadagno non è sufficiente , da solo, a caratterizzare completamente la distanza del sistema dal limite di instabilità. Nella figura sono infatti mostrati i diagrammi di Nyquist di due sistemi caratterizzati dallo stesso margine di guadagno ( stessa lunghezza del segmento PC , in quanto intersecano il semiasse reale negativo nello stesso punto ) : nonostante ciò , è evidente che il sistema tracciato in rosso è più prossimo all’instabilità del sistema tracciato in blu . In altre parole, nel sistema in rosso è sufficiente un minore incremento di Kst per ottenere un sistema a ciclo chiuso instabile , mentre per il sistema tracciato in blu è necessario un incremento maggiore . | |
 | |
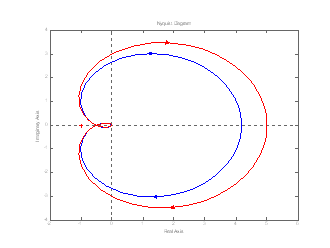Risulta utile, allora, definire una seconda grandezza che sia in grado di distinguere fra queste due situazioni. Per fare ciò si parte da una considerazione simile a quella effettuata per definire il margine di guadagno : il circondamento del punto critico avviene , per sistemi a retroazione unitaria, quando il modulo della funzione di trasferimento in catena aperta diventa pari ad 1. Definiamo pulsazione di attraversamento ,  , la “frequenza” per cui ciò accade :  .Possiamo pensare la pulsazione di attraversamento come la pulsazione in corrispondenza della quale il diagramma di Nyquist interseca la circonferenza unitaria : se in corrispondenza di la fase è inferiore a -180° l’intersezione avviene nel 3° quadrante ( figura 6A ) e il punto critico non viene circondato , perciò il sistema a ciclo chiuso è stabile. Se invece in corrispondenza di la frequenza è inferiore a -180° l’intersezione con la circonferenza unitaria avviene nel 2° quadrante e il punto critico viene circondato : il sistema a ciclo chiuso è instabile ( figura 6B ). | |
  | |
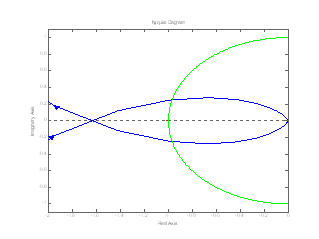Risulta quindi naturale definire il margine di fase come la “distanza” fra la fase della funzione di trasferimento alla pulsazione di attraversamento e il valore critico di -180°: |
Sommario completo degli appunti di Controlli Automatici:
Proprietà del Controllo in Controreazione
I requisiti di un sistema di controllo
La stabilità dei sistemi di controllo
La stabilità dei sistemi a ciclo chiuso
Come tracciare i diagrammi di Nyquist
Margine di fase e margine di guadagno
Sintesi di un sistema di Controllo di Tipo K
Sintesi diretta di un sistema a tempo continuo
Stabilità e fisica realizzabilità di un sistema di controllo progettato con la sintesi diretta
