I diagrammi di Bode consistono nella rappresentazione di modulo e fase della funzione di trasferimento al variare della frequenza del segnale di ingresso. Rispetto ai diagrammi polari o di Nyquist , presentano due sostanziali differenze:
1) fanno riferimento alla rappresentazione geometrica dei numeri complessi ( modulo e fase ) , mentre i diagrammi di Nyquist presentano sull’asse delle ascisse e su quello delle ordinate rispettivamente parte reale e parte immaginaria ( rappresentazione algebrica )2) presentano la frequenza ( o la pulsazione ) come variabile indipendente sull’asse delle ascisse , mentre nei diagrammi polari la pulsazione parametrizza la curva. Inoltre , per semplificare la rappresentazione grafica, l’asse delle ascisse ha scala logaritmica :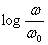 con con  da scegliere in base alle costanti di tempo del sistema da analizare ( solitamente 1 rad/s) . Anche l’asse delle ordinate , per il diagramma del modulo , ha scala logaritmica espressa in decibel : da scegliere in base alle costanti di tempo del sistema da analizare ( solitamente 1 rad/s) . Anche l’asse delle ordinate , per il diagramma del modulo , ha scala logaritmica espressa in decibel : Nel diagramma della fase, invece , l’asse delle ordinate ha scala lineare e vi si riporta  in gradi o radianti. in gradi o radianti. | |
| Tracciare i diagrammi di Bode | |
| A differenza dei diagrammi di Nyquist, i diagrammi di Bode si prestano abbastanza facilmente ad essere tracciati quantitativamente senza il ricorso a sistemi di calcolo automatico , grazie soprattutto a due semplificazioni: | |
| 1) | Il diagramma di Bode di una funzione di trasferimento si può costruire come sovrapposizione dei diagrammi di Bode dei singoli contributi : costante moltiplicativa, derivatori , integratori, poli e zeri semplici, coppie di poli e zeri complessi coniugati. Per la fase, come si è visto nella dimostrazione del lemma del mapping, vale la sovrapposizione degli effetti : se F(s) è nella forma  allora la fase della F(s) vale :  ;Per quanto riguarda il modulo, invece, la sovrapposizione degli effetti è dettata dall’utilizzo dei dB ; per le proprietà dei logaritmi , infatti , il prodotto dei moduli dei singoli contributi si traduce nella somma dei singoli contributi, espressi in dB : ;Per quanto riguarda il modulo, invece, la sovrapposizione degli effetti è dettata dall’utilizzo dei dB ; per le proprietà dei logaritmi , infatti , il prodotto dei moduli dei singoli contributi si traduce nella somma dei singoli contributi, espressi in dB :  |
| 2) | I diagrammi di Bode dei singoli contributi si possono tracciare in modo qualitativo con tratti spezzati, ricorrendo poi a dei diagrammi di correzione per risalire all’andamento quantitativamente corretto , mostrati in figura 1 per il caso di una coppia di zeri ( o poli , basta invertire l’asse delle ordinate ) complessi coniugati. |
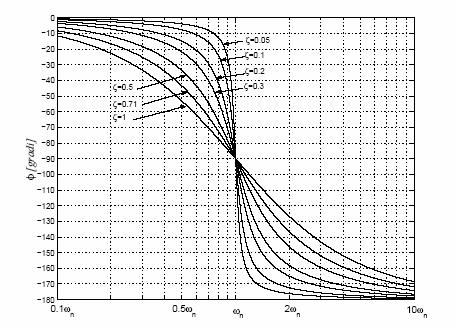 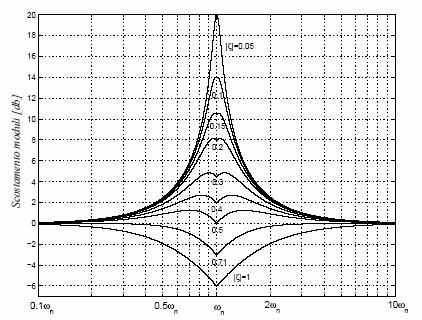 | |
| Di seguito sono riportati i diagrammi di Bode ( esatti ed approssimati , o asintotici ) dei singoli contributi che si possono presentare nel tracciare il diagramma complessivo di una qualsiasi funzione di trasferimento : | |
| costante moltiplicativa : esprimendo F(s) come prodotto di fattori , la costante k da luogo ad un modulo in dB pari a e ad una fase che vale : a1) 0 se k>0 ( come mostrato con il tratto blu in figura 2 ) a2) -180° se k<0 ( come mostrato con il tratto rosso in figura 2) | |
 | |
Zeri nulli :ciascun derivatore da un contributo rettilineo ( su scala logaritmica ) per quanto riguarda il modulo , con pendenza pari a 20dB/decade e un contributo alla fase pari a 90° ; ricordando come si calcola il modulo di un numero complesso , si ha infatti :  ;ricordando invece come si calcola la fase, e notando che la parte reale del termine derivato è nulla, si ha : ;ricordando invece come si calcola la fase, e notando che la parte reale del termine derivato è nulla, si ha :  .in figura 3 sono rappresentati un derivatore semplice in blu ( 20dB/dec e 90° ), un derivatore doppio in rosso ( 40dB/dec e +180° di sfasamento) e un triplo polo zero in verde ( 60dB/dec e 270° di sfasamento in anticipo ). {loadposition adsense_negli_articoli} .in figura 3 sono rappresentati un derivatore semplice in blu ( 20dB/dec e 90° ), un derivatore doppio in rosso ( 40dB/dec e +180° di sfasamento) e un triplo polo zero in verde ( 60dB/dec e 270° di sfasamento in anticipo ). {loadposition adsense_negli_articoli} | |
 | |
| poli nulli :con considerazioni simili a quelle viste per il derivatore, si può dimostrare che ciascun iintegratore contribuisce al modulo della funzione di trasferimento con un termine rettilineo a pendenza negativa di -20dB/decade e alla fase con un contributo costante di -90° ; in figura 3 sono rappresentati un integratore semplice in blu ( -20dB/dec e -90° ), un integratore doppio in rosso ( -40dB/dec e -180° di sfasamento) e un triplo polo nullo in verde ( -60dB/dec e -270° di sfasamento in anticipo ). | |
 | |
zeri reali non nulli :in figura 6 sono riportati il contributo al modulo e alla fase di un zero reale non nullo ; in rosso è riportato l’andamento di uno zero negativo, in blu quello di uno zero positivo. In celeste è invece riportato l’andamento del diagramma di bode approssimato , detto anche diagramma di Bode asintotico, che approssima l’andamento della fase e del modulo con delle spezzate. I diagrammi asintotici approssimano con buona precisione i diagrammi reali alle alte frequenze e alle basse frequenze , mentre intorno alla frequenza naturale dello zero introducono un errore massimo di 3dB per il modulo e di 5.7° per la fase . Matematicamente le approssimazioni sono spiegate dai seguenti passaggi : l’espressione del modulo in dB è  , dove si è definito , dove si è definito  , e:d1) alle basse frequenze , e:d1) alle basse frequenze  , per cui il modulo è pressoché nullo , per cui il modulo è pressoché nullo d2) alle alte frequenze  e si è visto, analizzando il contributo del derivatore, che tale espressione corrisponde ad una pendenza positiva di 20dB/decade. e si è visto, analizzando il contributo del derivatore, che tale espressione corrisponde ad una pendenza positiva di 20dB/decade.L’espressione della fase è invece :  e :d1) alle basse frequenze e :d1) alle basse frequenze  d2)alle alte frequenze  In caso di poli e zeri multipli , le pendenze del contributo del modulo e le fasi alle basse frequenze si sommano. {loadposition adsense_negli_articoli} | |
 | |
| e) | poli reali non nulli : per i poli reali non nulli valgono considerazioni simili a quelle viste per gli zeri non nulli. In figura 7 sono riportati gli andamenti reali per polo negativo ( rosso ) e polo positivo ( blu ) , mentre in celeste è riportato il diagramma asintotico costruito mediante spezzate. Va notato che , mentre nel diagramma del modulo di uno zero non nullo, la spezzata resta costantemente al di sotto dell’andamento esatto , per cui la correzione da apportare è di +3dB in corrispondenza di  , nel diagramma del polo è l’andamento reale ad essere minorato dalla spezzata, per cui la correzione da apportare è di -3dB. Come per lo zero, inoltre, la pendenza della seconda spezzata si raddoppia nel caso di polo doppio ( -40dB/decade ) si triplica per per polo triplo ( -60dB/decade ), ecc.. , nel diagramma del polo è l’andamento reale ad essere minorato dalla spezzata, per cui la correzione da apportare è di -3dB. Come per lo zero, inoltre, la pendenza della seconda spezzata si raddoppia nel caso di polo doppio ( -40dB/decade ) si triplica per per polo triplo ( -60dB/decade ), ecc.. |
 | |
| Rilevare margine di fase e margine di guadagno sui diagrammi di Bode | |
| Come nei diagrammi di Nyquist, il margine di fase ed il margine di guadagno hanno un immediato significato geometrico anche nei diagrammi di Bode. A differenza dei diagrammi polari, però, nei diagrammi di Bode è più agevole valutare quantitativamente queste due grandezze. 1) Il margine di guadagno può essere valutato in due semplici passi, che sono rappresentati in figura 8: 1a) Si individua della pulsazione  , definita dall’equazione , definita dall’equazione  , come intersezione fra il diagramma della fase e la linea tratteggiata verde in figura ; , come intersezione fra il diagramma della fase e la linea tratteggiata verde in figura ; 1b) Si valuta , sul diagramma del modulo, l’ampiezza del segmento congiungente ( lungo la verticale ) l’asse 0dB (linea tratteggiata celeste ) con il diagramma stesso. Se il segmento è contenuto nel semipiano dB<0 , il margine è positivo, altrimenti il margine di guadagno è negativo.2) Il margine di fase può essere può essere ricavato con una procedura simile : 2a) Si individua la pulsazione  , definita in precedenza come , definita in precedenza come  , dall’intersezione fra il diagramma del modulo e la linea tratteggiata celeste ( asse delle ascisse del primo diagramma , corrispondente ad una retta a modulo costante 0dB ) , dall’intersezione fra il diagramma del modulo e la linea tratteggiata celeste ( asse delle ascisse del primo diagramma , corrispondente ad una retta a modulo costante 0dB )2b) Si valuta l’ampiezza del segmento che congiunge , nel grafico della fase , il punto del diagramma in tale frequenza con la retta a fase costante -180° : il margine va considerato positivo se il punto si trova sopra la retta , negativo altrimenti. {loadposition adsense_negli_articoli} | |
 | |
Sommario completo degli appunti di Controlli Automatici:
Proprietà del Controllo in Controreazione
I requisiti di un sistema di controllo
La stabilità dei sistemi di controllo
La stabilità dei sistemi a ciclo chiuso
Come tracciare i diagrammi di Nyquist
Margine di fase e margine di guadagno
Sintesi di un sistema di Controllo di Tipo K
Sintesi diretta di un sistema a tempo continuo
Stabilità e fisica realizzabilità di un sistema di controllo progettato con la sintesi diretta